Some months ago, I went with my family to the Alexander Calder exhibit at MOCA Chicago. The collection was impressive, dozens of his collages and a few sculptures for good measure.
Afterwords, as we were eating our ice cream, my father wondered aloud whether how much calculation or adjustment Calder would have had to do, to get things to balance out. My off-the-cuff answer at the time was that only the last, smallest leaf would have to be correct, but I’ve since started to doubt whether that was correct.
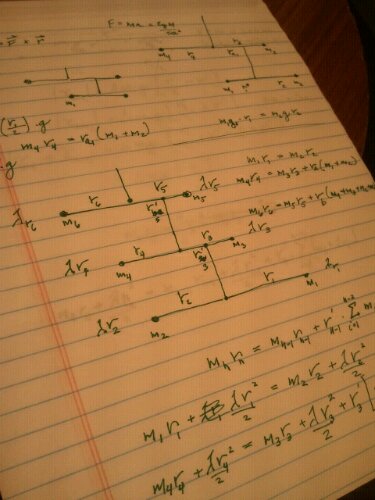
You know what Newton would be doing right now if he were alive? Clawing at the lid of his coffin. Recall that torque is equal to the vector cross product of force and radius vectors:
If your physics is a little rusty, intuitively you know that to double the torque you could use twice as much force or double the length of the lever, right? In our case, the force is due to gravity, and thus equal to the mass times the acceleration due to gravity:
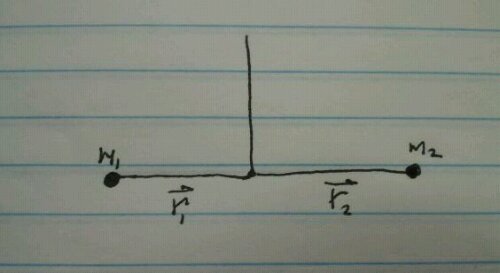
So for a very simple mobile with one arm and two weights such as the following:
This mobile will be in balance when:
![]() Some simplifying assumptions: We’re really only interested in the magnitude of the torque here, and let’s assume that each bar is hanging roughly horizontally and so the force and radius vectors are at a 90 degree angle. In which case, we can just multiply the scalar magnitudes of the terms together, and forgo the vector cross product. I’m not even sure I remember how to do a cross product, so this is a happy accident. Also, notice that each term in the above equation is multiplied exactly once by gravity, so we can just pull it out of both sides of the equation and forget about it. Then we have:
Some simplifying assumptions: We’re really only interested in the magnitude of the torque here, and let’s assume that each bar is hanging roughly horizontally and so the force and radius vectors are at a 90 degree angle. In which case, we can just multiply the scalar magnitudes of the terms together, and forgo the vector cross product. I’m not even sure I remember how to do a cross product, so this is a happy accident. Also, notice that each term in the above equation is multiplied exactly once by gravity, so we can just pull it out of both sides of the equation and forget about it. Then we have:
m1·r1 = m2·r2
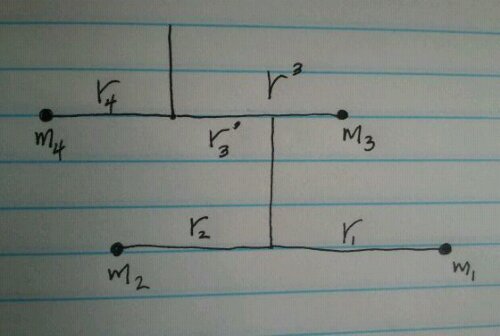
e.g. a 3 kg weight on a 2 meter arm would be in balance with a 6 kg weight on a 1 meter arm, right? Both sides of the equation would multiply out to 6 kg·m. The general solution for a 4-weight system such as:
m4·r4 = m3·r3 + r’3(m1 + m2)
Notice that the length of the lower arms become unimportant in balancing the upper arms– only the magnitude of the weights and the distance r’3 contribute to the system torque. More generally, for an arbitrarily large number of arms:
Perfect vacuums and frictionless pulleys: Of course, this isn’t Physics 101 and we can’t neglect the weight of the arms. Say that the arm material has a linear density of λ (kg per m would be the units). Then the weight of each arm is:
λ·ri
My sense is that this figure would only matter in aggregate, as the sum of all the arm mass vs. the largest weight on the top. Then the last equation becomes:
Elegant special case: If the arms are all of equal length, and each mass is twice as large as the one below it, e.g. mi = 2·mi-1, equation (1) above becomes one of my favorite geometric series (because I play favorites):
Or in diagram form:
 I think that a lot of what makes Calder’s mobiles so immediately appealing is in the orderly way that the proportions step down from one branch to the next.
I think that a lot of what makes Calder’s mobiles so immediately appealing is in the orderly way that the proportions step down from one branch to the next.
We now return to our original hypothesis, that only the last weight must be correct to balance out to make the mobile come out in balance: sort of true, but not really. Pulling out the first mass from equation (1):
m1 can be chosen so as to balance the equation, as can any other term for that matter. r1 can then be chosen so as to balance out m2·r2, but that’s as far as it goes– the second level consisting of m3·r3 and m4·r4 will need some entirely different mass to level out. It would be very difficult to build from the top and leave the final balancing until the end– every mass added would throw the balance off for the system above it. In fact, I think we can say with some confidence that Calder would have had to build his mobiles from the bottom up rather than the top down. So that’s kind of an interesting result.



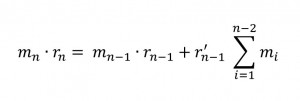
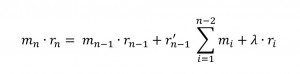
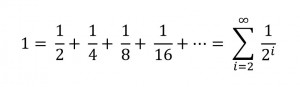
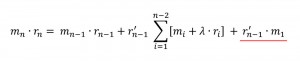
Nice post! I am doing a degree in secondary teaching, and I was thinking to develop an activity for mathematics with this kind of materials, after having seen a Calder sculpture in the Mudeum of Bilbao. Your post will be helpfull.
Yes, thanks! Great essay! Calder did this intuitively though, didn’t he? Re: Since it’s not physics 101 and you did mention lambda, the linear density of the arm, wouldn’t you (theoretically) have to also consider changes in the length of the arm (r) due to thermal expansion and contraction of the arm too? Thus each mass’s torque varies with temperature. A chilly Calder behaves subtly different than a cozy one.
Hi Max!
It’s seems to me that it gets more complicated than that when you consider the mass of the arms. In the equation for arm number n, the combined mass of all the other arms is indeed applied at one point (r’_n-1). But you also have to consider the mass of arm number n, which makes the problem in part continuous rather fully discret (an infinity of infinitesimal masses applied at infinitely many different points). I feel you would have to solve that with an integral. I might be wrong though!